Learning when Test and Training Inputs have Different Distributions Challenge

What is it about?

The goal of this challenge is to attract the attention of the Machine Learning community towards the problem where the input distributions, p(x), are different for test and training inputs. A number of regression and classification tasks are proposed, where the test inputs follow a different distribution than the training inputs. Training data (input-output pairs) are given, and the contestants are asked to predict the outputs associated to a set of validation and test inputs. Probabilistic predictions are strongly encouraged, though non-probabilitic “point” predictions are also accepted. The performance of the competing algorithms will be evaluated both with traditional losses that only take into account “point predictions” and with losses that evaluate the quality of the probabilistic predictions.

Results

We are proud to announce the two challenge winners:

Congratulations!

For a summary of the results, click on the “Results” tab.

How do I participate?

The first phase of the challenge is over, the results are summarized in the “Results” tab.
It is still possible to submit predictions and get them evaluated by the challenge server!

Download the datasets (“Datasets” in left frame)
Look at the evaluation criteria (“Evaluation”)
Format your predictions on the test inputs as required (“Instructions”)
Submit your results (“Submission”)
See how well you do compared to others (“Results”)

Where can we discuss the results?

There will be a workshop on this topic at the NIPS*2006 conference. The results of the competition will be announced there as well. More information about the workshop can be found here.

Background

Many machine learning algorithms assume that the training and the test data are drawn from the same distribution. Indeed many of the proofs of statistical consistency, etc., rely on this assumption. However, in practice we are very often faced with the situation where the training and the test data both follow the same conditional distribution, p(y|x), but the input distributions, p(x), differ. For example, principles of experimental design dictate that training data is acquired in a specific manner that bears little resemblance to the way the test inputs may later be generated.

The open question is what to do when training and test inputs have different distributions. In statistics the inputs are often treated as ancillary variables. Therefore even when the test inputs come from a different distribution than the training, a statistician would continue doing “business as usual”. Since the conditional distribution p(y|x) is the only one being modelled, the input distribution is simply irrelevant. In contrast, in machine learning the different test input distribution is often explicitly taken into account. An example is semi-supervised learning, where the unlabeled inputs can be used for learning. These unlabeled inputs can of course be the test. Additionally, it has recently proposed to re-weight the training examples that fall in areas of high test input density for learning (Sugiyama and Mueller, 2005). Transductive learning, which concentrates the modelling at the test inputs, and the problem of unbalanced class labels in classification, particularly where this imbalance is different in the training and in the test sets, are both also very intimately to the problem of different input distributions.

It does not seem to be completely clear, whether the benefits of explicitly accounting for the difference between training and test input distributions outweigh the potential dangers. By focusing more on the training examples in areas of high test input density, one is effectively throwing away training data. Semi-supervised learning on the other hand is very dependent on certain prior assumptions being true, such as the cluster assumption for classification.

The aim of this challenge is to try and shed light on the kind of situations where explicitly addressing the difference in the input distributions is beneficial, and on what the most sensible ways of doing this are. For this purpose, we bring the theoretical questions to the empirical battleground. We propose a number of regression and classification datasets, where the test and training inputs have different distributions.

Deadline and Number of Submissions

The deadline for final submissions is November 24, 2006.
Please observe limit of at most 5 submissions per day on a given dataset.

Instructions for Submission

One submission is associated to one dataset, and consists of a file compressed with “zip”. The name of the compressed file is irrelevant, only its extension is important.
Zip programs are available for most operating systems, including Microsoft Windows, Linux and Mac OS. If, however, you do not have a zip program installed on your system yet, you can find download links on the tools page.
The compressed file should contain one ascii file for each split of the data (training, validation and test). The names are important, and must follow the following convention:
- datasetname_train_predict.txt
- datasetname_val_predict.txt
- datasetname_test_predict.txt (only after November 10)
Example: to submit your results for the “barley” dataset do
> zip results.zip barley_train_targets.txt barley_val_targets.txt barley_test_targets.txt

Validation phase and test phase

Until November 10, the challenge will be in its validation phase: only the validation inputs will be available, and therefore only the validation predictions will be evaluated. On November 10, the test inputs will be released, as well as the validation targets, and the test phase will start, which will last until the deadline for submissions of November 24. During the validation phase, the losses of the submissions will be immediately displayed in the results page. During the test phase however, no results will be shown. This is to avoid the temptation of fine tuning the algorithms by using the feedback provided by the test score. The final ranking will be built according to the test scores. During the validation phase, submissions will be ranked according to the validation score, to allow participants to get an idea of how their method does.

Format of the ASCII files

Both for regression and classification, the ASCII files should contain one prediction per row.
The predictions must be made in the same order as the inputs appear in the data files. For example, the file “barley_val_predict.txt” should contain 300 rows, as many as validation examples.
Exponential notation is accepted, in the form 6.7125064e-01.
(Matlab’s default when saving to ASCII files)

Classification

For classification, one prediction is equal to $p(y_j=+1\vert x_j)$ , which is a number in corresponding to the estimated (posterior) probability of input of belonging to class ““.
To produce non-probabilistic predictions in classification, just return “hard” probabilities of belonging to class “+1”, equal to either “1” or to “0”.

Regression

For regression, one prediction is a set of numbers that describe some aspects of the predictive distribution $p(y_j\vert x_j)$ .

by providing the mean and variance of a Gaussian predictive distribution:To declare that the mean and variance of a Gaussian predictive distribution are specified, the corresponding row of the ASCII file must start with a “” and then contain the mean and the variance. For example, if the estimated $p(y_j\vert x_j)$ has mean and variance , the j-th line of the ASCII file should be: $\lq\lq \,1 \quad 3.1 \quad 1.7\,''$ To produce non-probabilistic predictions in regression, produce Gaussian predictions with the mean equal to your “point prediction”, and the variance equal to 0.
by providing a set of quantiles that describe the predictive distribution:To use quantiles to describe the predictive distribution, the corresponding row of the ASCII file should start with a ““, and be followed by a number of pairs of probabilities and associated quantiles. To describe the estimated predictive distribution with quantiles, the j-th row of the ASCII file should look like: $\lq\lq \,0 \quad \alpha_1 \quad q_{\alpha_1} \quad \alpha_2 \quad q_{\alpha_2} \quad \ldots \quad \alpha_N \quad q_{\alpha_N}\,''$ where for all the $\alpha_k$ ‘s are cumulative probabilities that obey $0 < \alpha_k < \alpha_{k+1} < 1$ , and the participant is free to choose their number (although 200 is the maximum) () and their values.For a given $\alpha_k$ , the corresponding quantile $q_{\alpha_k}$ is computed from the predictive (of the true target distribution) as:

$\begin{displaymath} p(y_j < \alpha_k\vert x_j) = \alpha_k \end{displaymath}$ (1)

It is possible to use both ways of describing prediction distributions for different predictions in the same ASCII file.

Datasets for Classification

Name	Size	Features	Training Examples	Validation Examples	Test Examples	Link
Wheat	37 KB	5	400	50	1000
Barley	37 KB	5	400	50	1000
Schnitzel	5 KB	3	280	40	185

Format of the datasets

Each dataset is contained in a folder compressed with zip
Each dataset comprises 3 ascii files named
- [dataset_name]_train_inputs.txt
- [dataset_name]_train_targets.txt
- [dataset_name]_val_inputs.txt
Rows correspond to examples, columns to dimensions

NEW! (13.11.06) The final version of the datasets has been released. You need to download the whole data again

On November 10, a new version of the datasets will be released, which will include the two following files in addition to the above:

[dataset_name]_val_targets.txt (available after November 10)
[dataset_name]_test_inputs.txt (available after November 10)

to obtain them, you will have to download the datasets again from this page.

Script for computing losses

You can download a python script called ‘evaluate.py’ for computing the different losses [here]

Usage:
>> python evaluate.py your_prediction_file true_targets_file loss_type

where loss_type is a number from 1 to 4 with the meaning:

Regression: 1 = NLPD, 2 = MSE
Classification: 3 = NLP, 4 = 01L

The files with your predictions and with the true targets should be formatted in the usual way for this challenge.

Measures for Evaluation of Performance

We plan to use losses that both allow to evaluate the quality of the predictive distributions, and standard losses that evaluate deterministic predictions.

Suppose in all cases that there are test (or validation) input/output pairs: $\{x_i,y_i\}_{i=1,...,n}$

Ranking

For each dataset, the methods of the participants will be ranked from best to worst.

The test performance will not be evaluated until after the deadline for submission (November 24, 2006).
In the meantime, the methods will be ranked according to their NLP (see below) performance on the validation set.
One week before the deadline for submissions the targets of the validation set will be made public for the use of the participants.

Losses for Classification

In classification, the true labels can only take values “” or ““. We use the following two losses:

[NLP] Average negative log estimated predictive probability of the true labels:

$\begin{displaymath} L = - \frac{1}{n} \left[\sum_{\{i\vert y_i=+1\}} \log p( y_i... ...t y_i=-1\}} \log \left[1 - p( y_i=+1 \vert x_i )\right]\right] \end{displaymath}$ (1)

Notice that this loss penalizes both over and under-confident predictions. Over-confident predictions can be infinitely penalized, so we discourage contestants to submit predictive probabilities equal to 1. Zero is the minimum value of this loss, that one could achieve if one predicted correctly with 100% confidence. If one predicts otherwise, the worse one predicts, the larger the loss. This loss is also referred to as “negative cross-entropy loss”.
[01L] Average classification error (0/1 loss):

$\begin{displaymath} L = \frac{1}{n} \left[\sum_{\{i\vert y_i=+1\}} {\mathbf 1} \... ...t y_i=-1\}} {\mathbf 1}\{p(y_i=+1\vert x_i) < 0.5\} \right], \end{displaymath}$ (2)

where ${\mathbf 1}\{\cdot\}$ is the indicator function.
This is the classic 0/1 loss, obtained by thresholding the predictive probabilities about 0.5. Its minimum value is 0, obtained when no test (or validation) examples where missclassified; it is otherwise equal to the fraction of missclassified examples relative to the total number of examples.

Losses for Regression

In regression, the true labels are real valued numbers. We use the following two losses:

[NLPD] Average negative log estimated predictive density of the true targets:

$\begin{displaymath} L = \frac{1}{n} \sum_{i=1,\ldots,n} \log p( y_i \vert x_i ) \end{displaymath}$ (7)

This measure penalizes over-confident predictions as well as under-confident ones.
[MSE] Mean squared error (normalized):

$\begin{displaymath} L = \frac{1}{n} \sum_{i=1,\ldots,n} ( y_i - m_i )^2 \end{displaymath}$ (8)

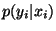where is the mean of the estimated predictive distribution $p( y_i \vert x_i )$ . We normalize the loss by the empirical variance of the training data, $\operatorname{var}(y)$ . This classical loss takes only into account a point prediction that minimizes squared errors. Given the predictive distribution, this optimal point prediction is its mean.

How are the losses obtained from quantiles?

If the participant describes a predictive distribution by a Gaussian (mean and variance), the losses for regression are straightforward to compute.
If the participant describes a predictive distribution by a number of quantiles, we approximate the density at the true target, and we obtain an approximation to the predictive mean. Please find the details in the following document [pdf]

Summary of the Results

We are proud to announce the two challenge winners:

Congratulations!

In the following, we list the best 3 submissions for each data set, based on the submissions that were received until November 24, 2006. For updated results that also include submissions after November 24, click here (classification) or or here (regression).

Udon (Regression)

“Udon” are samples from a noisy sine function. The data set is inspired by the toy data set in Sugiyama and Mueller (2006), where the function suddenly changes from sine to linear right at the border between training and test data. Here, this slightly surprising change does not occur.

(Udon)

Udon: Best 3 submissions
Method	NLPD	MSE	Author
submission #1	-6.461e-1	1.984e-3	Gavin Cawley
submission #2	-6.38e-1	2.942e-3	Gavin Cawley
baseline	1.154	9.989e-1
Submission 1	—	6.849e-3	Ray, Debajyoti
baseline, non-prob	—	9.989e-1

A number of people only submitted results for validation data (Jukka Kohonen, Cyril Goutte).

Gavin Cawley writes about his winning submission: “simple sinusoidal model with parameters representing the amplitude, frequency and offset. Fitted using leave-one-out cross- validation. The variance estimator was augmented by a component representing the variance of the leave-one-out estimates, to give a slightly heteroscedastic variance (although this didn’t make much difference).”

Maki (Regression)

Maki represents a depth from stereo experiment. Actually, this is an ordinal regression dataset – still, we evaluate it as standard regression. The difficulty here is that training data were chosen only from a number of planes, wheres test data are chosen from all planes.

Maki: Best 3 submissions
Method	NLPD	MSE	Author
submission #3	6.486e-1	8.028e-5	Gavin Cawley
submission #4	7.723e-1	7.333e-5	Gavin Cawley
submission #5	7.896e-1	7.191e-5	Gavin Cawley
baseline	4.979	1.003
baseline, non-prob	—	1.003

Gavin Cawley writes about his winning submission: “They are all kernel ridge regression models, with the regularisation and kernel parameters set so as to minimise the leave-one-out error. #1: linear, #2: quadratic, #3: cubic, #4: rbf, #5: rbf with feature scaling”

Schnitzel (Classification)

Here comes the real world! The Schnitzel data set stems from a Brain-Computer-Interface (BCI) experiment (“Schnitzel” is the nickname of the subject in this experiment).

Training data stem from the BCI training session, validation and test data were taken from the BCI feedback session. The big challenge here is that training and test exhibit neurophysiological differences. Thus, this data set is actually an “outlier”, in that not only the input distribution of training and test is different, but also the conditional distribution changes.

So, in a way, this is Mission Impossible. The baseline achievable here (classifier on training data only) is around 40% error rate. With a classifier that does a sequential update when test targets become available, it is possible to reach around 32% error rate.

Schnitzel: Best 3 submissions (Probabilistic Loss)
Method	NLPD	0/1 Loss	Author
baseline	6.931e-1	5.351e-1
submission #1	7.765e-1	5.081e-1	Gavin Cawley
Submission 1	7.786e-1	3.946e-1	Ray, Debajyoti
submission #2	8.037e-1	4.378e-1	Gavin Cawley

Schnitzel: Best 3 submissions (Nonprobabilistic Loss)
Method	0/1 Loss	Author
Submission 2	3.838e-1	Ray, Debajyoti
Submission 1	3.946e-1	Ray, Debajyoti
submission #4	4.378e-1	Gavin Cawley
baseline, non-prob	5.351e-1
baseline	5.351e-1

Gavin Cawley writes about his submission: “performed a PCA (on all three sets) and discarded the first principal component (as the training data has discriminative informaation in this direction that was not compatible with the test and validation sets having many positive patterns). I think submissions 1 and 2 are just kernel logistic regression models. A logistic regression model was used, with a simple form of Baysian transduction on submission #4.”

Barley (Classification)

Barley is the 5-dimensional version of the following data set: (blue and black are the training data, red is the test data)

(Barley in 2D)

Barley: Best 3 submissions (Probabilistic Loss)
Method	NLPD	0/1 Loss	Author
Submission 3	1.329e-1	3.7e-2	Ray, Debajyoti
Submission 2	1.336e-1	4e-2	Ray, Debajyoti
Submission 1	1.433e-1	4.3e-2	Ray, Debajyoti
baseline	1.164	6.42e-1

Barley: Best 3 submissions (Nonprobabilistic Loss)
Method	0/1 Loss	Author
Submission 3	3.7e-2	Ray, Debajyoti
Submission 2	4e-2	Ray, Debajyoti
submission #7	4.2e-2	Gavin Cawley
baseline	6.42e-1
baseline, non-probabilistic	6.42e-1

Gavin Cawley writes about his submission: “They are all kernel ridge regression models, with the regularisation and kernel parameters set so as to minimise the leave-one-out error, the kernels used are in the following order: #1 linear, #2 quadratic, #3 cubic, #4 rbf, #5 rbf with feature scaling. #6is logistic regresion with Bayesian transduction, but it needs work, it was a bit of a hack!”

Wheat (Classification)

Wheat is the 5-dimensional version of the following data set: (blue and black are the training data, red is the test data)

(Wheat in 2D)

Wheat: Best 3 submissions (Probabilistic Loss)
Method	NLPD	0/1 Loss	Author
submission #1	2.701e-1	1.38e-1	Gavin Cawley
Submission 1	2.817e-1	1.39e-1	Ray, Debajyoti
submission #3	2.819e-1	1.25e-1	Gavin Cawley
baseline	7.093e-1	6.33e-1

Wheat: Best 3 submissions (Nonprobabilistic Loss)
Method	0/1 Loss	Author
submission #3	1.25e-1	Gavin Cawley
submission #1	1.38e-1	Gavin Cawley
submission #7	1.38e-1	Gavin Cawley
basline, non-probabilistic	6.33e-1
baseline	6.33e-1

Gavin Cawley writes about his winning submission: ” They are all kernel ridge regression models, with the regularisation and kernel parameters set so as to minimise the leave-one-out error, the kernels used are in the following order: #1 linear, #2 quadratic, #3 cubic, #4 rbf, #5 rbf with feature scaling. #6is logistic regresion with Bayesian transduction, but it needs work, it was a bit of a hack!”