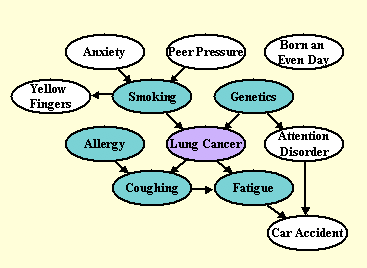
The focus of this challenge is on predicting the results of actions performed by an external agent. Examples of that problem are found, for instance, in the medical domain, where one needs to predict the effect of a drug prior to administering it, or in econometrics, where one needs to predict the effect of a new policy prior to issuing it. We focus on a given target variable to be predicted (e.g. health status of a patient) from a number of candidate predictive variables (e.g. risk factors in the medical domain). Under the actions of an external agent, variable predictive power and causality are tied together. For instance, both smoking and coughing may be predictive of lung cancer (the target) in the absence of external intervention; however, prohibiting smoking (a possible cause) may prevent lung cancer, but administering a cough medicine to stop coughing (a possible consequence) would not.
Setting
Most feature selection algorithms emanating from machine learning do not seek to model mechanisms: they do not attempt to uncover cause-effect relationships between feature and target. This is justified because uncovering mechanisms is unnecessary for making good predictions in a purely observational setting. Usually the samples in both the training and tests sets are assumed to have been obtained by identically and independently sampling from the same “natural” distribution.
In contrast, in this challenge, we investigate a setting in which the training and test data are not necessarily identically distributed. For each task (e.g. REGED, SIDO, etc.), we have a single training set, but several test sets (associated with the dataset name, e.g. REGED0, REGED1, and REGED2). The training data come from a so-called “natural distribution”, and the test data in version zero of the task (e.g. REGED0) are also drawn from the same distribution. We call this test set “unmanipulated test set”. The test data from the two other versions of the task (REGED1 and REGED2) are “manipulated test sets” resulting from interventions of an external agent, which has “manipulated” some or all the variables in a certain way. The effect of such manipulations is to disconnect the manipulated variables from their natural causes. This may affect the predictive power of a number of variables in the system, including the manipulated variables. Hence, to obtain optimum predictions of the target variable, feature selection strategies should take into account such manipulations.
To gain a better understanding of the tasks, we invite you to study our toy example causal network for the model problem of diagnosis, prevention, and cure of lung cancer:
Competition rules
- Conditions of participation: Anybody who complies with the rules of the challenge is welcome to participate. The challenge is part of the competition program of the World Congress on Computational Intelligence (WCCI08), Hong-Kong June 1-6, 2008. Participants are not required to attend the post-challenge workshop, which will be held at the conference, and the workshop is open to non-challenge participants. The proceedings of the competition will be published by the Journal of Machine Learning Research (JMLR).
- Anonymity: All entrants must identify themselves with a valid email address, which will be used for the sole purpose of communicating with them. Emails will not appear on the result page. Name aliases are permitted during the development period to preserve anonymity. For all final submissions, the entrants must identify themselves by their real names.
- Data: There are 4 datasets available (REGED, SIDO, CINA and MARTI), which have been progressively introduced, see the Dataset page. No new datasets will be introduced until the end of the challenge.
- Development period: Results must be submitted beween the start and the termination of the challenge (the development period). The challenge starts on December 15, 2007 and is scheduled to terminate on April 30, 2008.
- Submission method: The method of submission is via the form on the Submission page. To be ranked, submissions must comply with the Instructions. A submission may include results on one or several datasets. Please limit yourself to 5 submissions per day maximum. If you encounter problems with the submission process, please contact the Challenge Webmaster.
- Ranking: For each entrant, only the last valid entry, as defined in the Instructions will count towards determining the winner. Valid entries are found in the Overall table. The method of scoring is posted on the Evaluation page. If the scoring method changes, the participants will be notified by email by the organizers.
- Reproducibility: Everything is allowed that is not explicitly forbidden. We forbid using the test set for “learning from unlabeled data” [why?], that is for determining the structure and parameters of the model, including but not limited to learning variable causal dependencies from the test data, learning distribution shifts, and transduction. Participation is not conditioned on delivering your code nor publishing your methods. However, we will ask the top ranking participants to voluntarily cooperate to reproduce their results. This will include filling out a fact sheet about their methods and eventually participating to post-challenge tests and sending us their code, including the source code. The outcome of our attempt to reproduce your results will be published and add credibility to your results.
Challenge Datasets
We propose datasets from various application domains. We took great care of using real data. Some datasets encode real data directly, while others result from “re-simulation”, i.e. they were obtained from data simulators trained on real data. All datasets differing in name only by the last digit have the same training set. Digit zero indicates unmanipulated test sets. See the details of our data generating process.
| Dataset (click for info) | Description | Test data | Variables (num) | Target | Training examples | Test examples | Download (text format) | Download (Matlab format) |
|---|---|---|---|---|---|---|---|---|
| REGED0 | Genomics re-simulated data | Not manipulated | Numeric (999) | Binary | 500 | 20000 | 31 MB | 25 MB |
| REGED1 | Genomics re-simulated data | Manipulated (see list of manipulated variables) | Numeric (999) | Binary | 500 | 20000 | 31 MB | 25 MB |
| REGED2 | Genomics re-simulated data | Manipulated | Numeric (999) | Binary | 500 | 20000 | 31 MB | 25 MB |
| SIDO0 | Pharmacology real data w. probes | Not manipulated | Binary (4932) | Binary | 12678 | 10000 | 12 MB | 14 MB |
| SIDO1 | Pharmacology real data w. probes | Manipulated | Binary (4932) | Binary | 12678 | 10000 | 12 MB | 14 MB |
| SIDO2 | Pharmacology real data w. probes | Manipulated | Binary (4932) | Binary | 12678 | 10000 | 12 MB | 14 MB |
| CINA0 | Census real data w. probes | Not manipulated | Mixed (132) | Binary | 16033 | 10000 | 1 MB | 1 MB |
| CINA1 | Census real data w. probes | Manipulated | Mixed (132) | Binary | 16033 | 10000 | 1 MB | 1 MB |
| CINA2 | Census real data w. probes | Manipulated | Mixed (132) | Binary | 16033 | 10000 | 1 MB | 1 MB |
| MARTI0 | Genomics re-simulated data w. noise | Not manipulated | Numeric (1024) | Binary | 500 | 20000 | 47 MB | 35 MB |
| MARTI1 | Genomics re-simulated data w. noise | Manipulated | Numeric (1024) | Binary | 500 | 20000 | 47 MB | 35 MB |
| MARTI2 | Genomics re-simulated data w. noise | Manipulated | Numeric (1024) | Binary | 500 | 20000 | 47 MB | 35 MB |
A small example
We provide a small toy example dataset for practice purpose. You may submit results on these data on the Submit page like you would do for the challenge datasets. Your results will appear on the Result page, thus providing you with immediate feed-back. The results on these practice datasets WILL NOT COUNT as part of the challenge.
You may download all the example data as a single archive (Text format 1.1 MB, Matlab format 1.2 MB), or as individual datasets from the table below.
| Dataset (click for info) | Description | Test data | Variables (num) | Target | Training examples | Test examples | Download (text format) | Download (Matlab format) |
|---|---|---|---|---|---|---|---|---|
| LUCAS0 | Toy medicine data | Not manipulated | Binary (11) | Binary | 2000 | 10000 | 31 KB | 22 KB |
| LUCAS1 | Toy medicine data | Manipulated | Binary (11) | Binary | 2000 | 10000 | 31 KB | 22 KB |
| LUCAS2 | Toy medicine data | Manipulated | Binary (11) | Binary | 2000 | 10000 | 31 KB | 22 KB |
| LUCAP0 | Toy medicine data w. probes | Not manipulated | Binary (143) | Binary | 2000 | 10000 | 341 KB | 262 KB |
| LUCAP1 | Toy medicine data w. probes | Manipulated | Binary (143) | Binary | 2000 | 10000 | 342 KB | 654 KB |
| LUCAP2 | Toy medicine data w. probes | Manipulated | Binary (143) | Binary | 2000 | 10000 | 342 KB | 263 KB |
Dataset Formats
All datasets are formatted in a similar way. They include a training set from a “natural” distribution, in the form of a data table with variables in columns and samples in the rows. One particular column called “target” is singled out. A larger test set in the same format is provided, without the targets. The test set is not necessarily drawn from the same distribution as the training set. In particular, some variables may have been “manipulated”, i.e. an external agent may have set them to given values, therefore de facto disconnecting them from their natural causes.All data sets are in the same format and include 4 files in text format:
- dataname.param – Parameters and statistics about the data.
- dataname_train.data – Training set (a space delimited table with patterns in rows, features in columns).
- dataname_test.data – Test set (same format as training set).
- dataname_train.targets – Target velues for training examples.
For convenience, we also provide the data tables in Matlab format: dataname_train.mat and dataname_test.mat.
If you are a Matlab user, you can download some sample code to read and check the data.
How to format and ship results
Results File Formats
The results on each dataset should be formatted in text files according to the following table. If you are a Matlab user, you may find some of the sample code routines useful for formatting the data. You can view an example of each format from the filename column.
| Filename | Development | Final entries | Description | File Format |
|---|---|---|---|---|
| [dataname]_feat.ulist | Optional | Compulsory (unless [dataname]_feat.slist is given) | Unsorted list of N features used to make predictions. | A space-delimited unsorted list of variables/features used to make prediction of the target variable. The features are numbered starting from 1, in the column order of the data tables. |
| [dataname]_feat.slist | Optional | Compulsory (unless [dataname]_feat.ulist is given) | Sorted list of N features used to make predictions. | A space-delimited sorted list of variables/features, most likely to be predictive come first. The features are numbered starting from 1, in the column order of the data tables. The list should contain no repetition, but it may contain a subset of all features. As explained below, the list may be used to define nested subsets of n predictive features. |
| [dataname]_train.predict | Optional | Compulsory | Target prediction result table for training examples. | Target prediction values* for all M samples of the data tables. There are two possible formats: (1) a single column of M prediction values, obtained with all the features of [dataname]_feat.ulist or [dataname]_feat.slist, or (2) a space delimited table of predictions for a varying number of predictive features, with M lines and C columns. The second format may be used only in conjunction with a valid [dataname]_feat.slist file. Each column should represent the prediction values obtained with only the first n features of [dataname]_feat.slist, where n varies by powers of 2: 1, 2, 4, 8, … If the total number of features N in [dataname]_feat.slist is not a power of 2, the last column should correspond to using all N features. Hence C=log2(N)+1 or log2(N)+2. |
| [dataname]_test.predict | Compulsory | Compulsory | Target prediction result table for test examples. |
* If the targets are binary {+1, -1} values (two-class classification) the prediction values may either be binary {+1, -1} or discriminant positive or negative values (zero will be interpreted as a small positive value).
When you submit your results you get immediate feed-back on the Result page: a color code indicates in which quartile your performance lies. Explanations about the scoring measures are found on the Evaluation page.
IMPORTANT: To see your results in the “Overall” Result table, you must enter results for all the tasks whose data names differ only by the number in the same submission, e.g. for REGED, you must enter results for REGED0, REGED1, and REGED2. Only the entries figuring in that table will be considered for the final ranking and the challenge prizes.
Results Archive Format
Submitted files must be in either a .zip or .tar.gz archive format. You can download the example zip archive to help familiarise yourself with the archive structures and contents (the results were generated with the sample code). Submitted files must use exactly the same filenames as in the example archive. If you use tar.gz archives please do not include any leading directory names for the files. Use
zip results.zip *.predict *.slist [or *.ulist]
or
tar cvf results.tar *.predict *.slist [or *.ulist]; gzip results.tar
to create valid archives.
Evaluation
The main objective of the challenge is to make good predictions of the target variable. The datasets were designed such that the knowledge of causal relationships should help making better predictions in manipulated test sets. Hence, causal discovery is assessed indirectly via the test set performances or Tscore, which we will use for determining the winner. We also provide for information Fnum, Fscore, and Dscore, but will not use them for ranking participants. The scores found in the table of Results are defined as follows:
- Causal Discovery:
- Fnum: The number of features in [dataname]_feat.ulist or the best number of features used to make predictions with [dataname]_feat.slist.
- Fscore: Score for the list of features provided (see details below). For sorted lists [dataname]_feat.slist, the most predictive features should come first to get a high score. For unsorted lists [dataname]_feat.ulist, the features provided should be highly predictive to get a high score.
- Target Prediction:
- Dscore: Discovery score evaluating the target prediction values [dataname]_train.predict.
- Tscore: Test score evaluating the target prediction values [dataname]_test.predict.
Presently, for the datasets proposed, the Tscore and Dscore are the training and test AUC (which are identical to the BAC in the case of binary predictions).
During the development period, the scores are replaced by xxxx, except for the toy datasets, which do not count for the competition. A color coding indicates in which quartile your scores lie. The actual results will be made visible only after the end of the challenge.
Performance Measure Definitions
The results of classification, obtained by thresholding the prediction values made by a discriminant classifier, may be represented in a confusion matrix, where tp (true positive), fn (false negative), tn (true negative) and fp (false positive) represent the number of examples falling into each possible outcome:
| Prediction | |||
|---|---|---|---|
| Class +1 | Class -1 | ||
| Truth | Class +1 | tp | fn |
| Class -1 | fp | tn | |
We define the sensitivity (also called true positive rate or hit rate) and the specificity (true negative rate) as:
Sensitivity = tp/pos
Specificity = tn/neg
where pos=tp+fn is the total number of positive examples and neg=tn+fp the total number of negative examples.
Balanced ACccuracy (BAC) and Balanced Error Rate (BER)
The balanced accuracy is the average of the sensitivity and the specificity, obtained by thresholding the prediction values at zero:
BAC = 0.5*(tp/(tp+fn) + tn/(tn+fp)).
The balanced error rate is its complement to one: BER = (1-BAC)
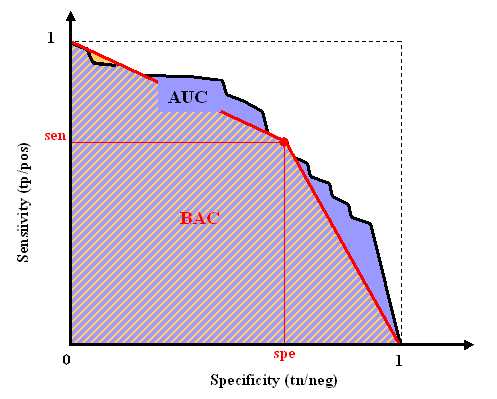
Area Under Curve (AUC)
The area under curve or AUC is defined as the area under the ROC curve. This area is equivalent to the area under the curve obtained by plotting sensitivity against specificity by varying a threshold on the prediction values to determine the classification result. The AUC is calculated using the trapezoid method. In the case when binary scores are supplied for the classification instead of discriminant values, the curve is given by {(0,1),(tn/(tn+fp),tp/(tp+fn)),(1,0)} and AUC = BAC.
Fscore
To provide a more direct evaluation of causal discovery, we compute various scores, which evaluate the fraction of causes, effects, spouses, and other features, which may be related to the target, in the feature set that you are using to make predictions. We will use those scores to analyze the results of the challenge. One of those, which we call Fscore, is displayed in the Result tables. The Fscore is computed in the following way:
- A set of “good” features is defined from the truth values of the causal relationships, known only to the organizers. This constitutes the “positive class” of the features. The other features belong to the “negative class”.
- The features returned by the participants as a ulist or an slist are interpreted as classification results into the positive or negative class. For a ulist, all the list elements are interpreted as classified in the positive class and all other features as classified in the negative class. For an slist, the feature rank is mapped to a classification prediction value, the features ranking first being mapped to a high figure of merit. If the slist does not include all features, the missing features are all given the same lowest figure of merit.
- The Fscore is the AUC for the separation “good” vs. “not-so-good” features. It is identical to the BAC in the case of a ulist.
- The definition of “good” feature depends on the dataset and whether the test data are manipulated of not.
- For artificial and re-simulated data (for which we know the all truth values of the causal relationships), the Test data Markov Blanket (MBT) is our chosen set of “good” features. The MBT generally does NOT coincides with the Discovery data Markov Blanket (MBD) of the natural distribution, from which discovery/training data are drawn, except if the test data were drawn from the same “unmanipulated” distribution.
- For real data with probes (for which we know only the truth values of the causal relationships between target and probes), the set of “not-so-good” features is the set of probes not belonging to the Markov blanket of the target, in test data. In the case of manipulated data, since we manipulate all the probes, the set of “not-so-good” features coincides with the set of all probes. In this last case, if we define Rscore (“real score”) as the score for the separation of real variable into “cause” vs. “non-cause”, under some conditions, the Fscore is asymptotically linearly related to the Rscore
Fscore = (num_true_pos/num_R) Rscore + 0.5 (num_true_neg/num_R)
where num_true_pos is the (unknown) number of features in the true positive class (real variables, which are causes of the target) and, num_true_neg is the umber of other real variables, and num_R is the total number of real variables.


